Tri Rose
ISeeDeadPixel
4.8 ★
store rating
500+
downloads
Free
AppRecs review analysis
AppRecs rating 4.8. Trustworthiness 0 out of 100. Review manipulation risk 0 out of 100. Based on a review sample analyzed.
★★★★☆
4.8
AppRecs Rating
Ratings breakdown
5 star
83%
4 star
17%
3 star
0%
2 star
0%
1 star
0%
What to know
✓
High user satisfaction
83% of sampled ratings are 5 stars
About Tri Rose
The original Math Rose app!
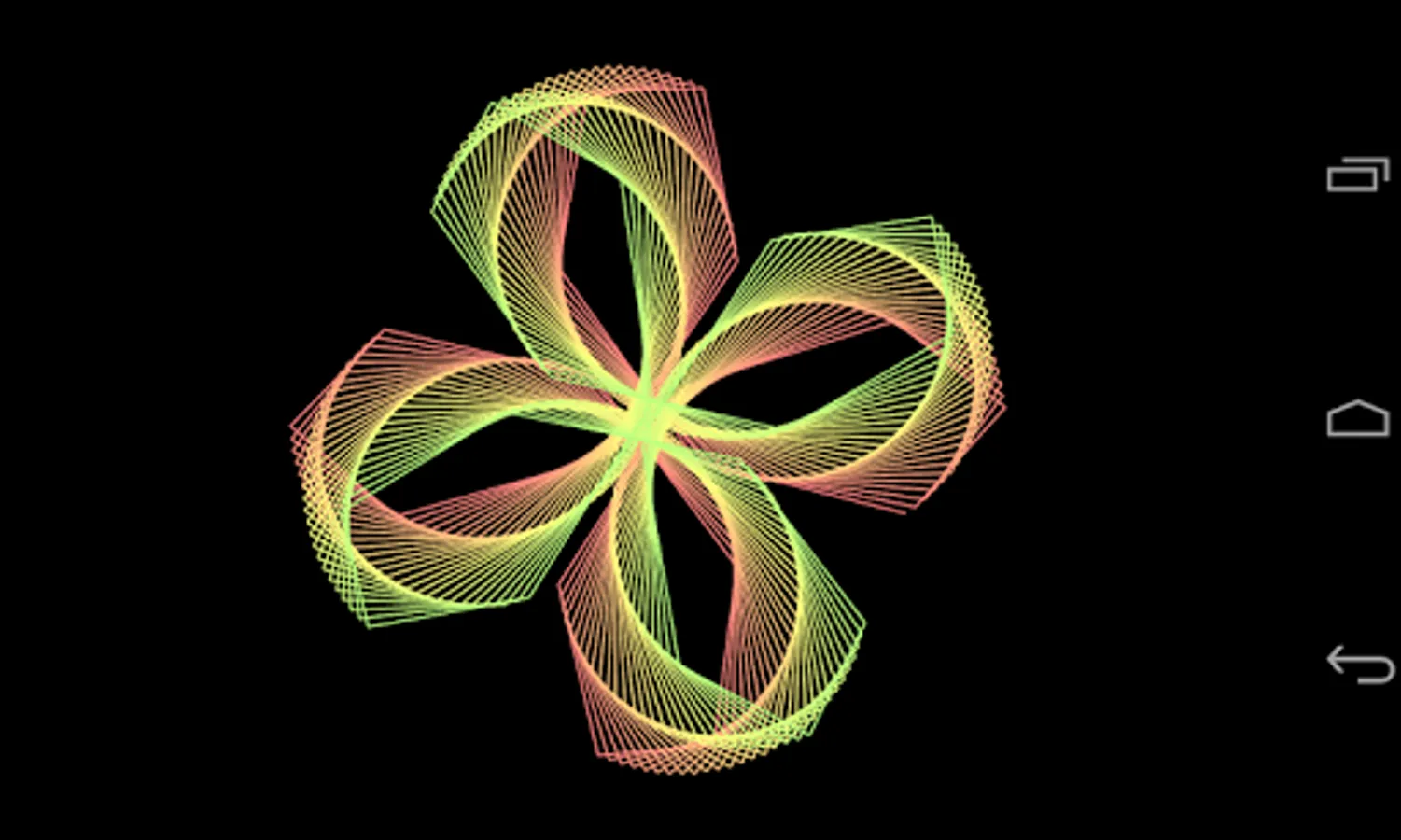
Mathematically generate unique and intricate rose graphs (rhodonea curves) and share them with your friends!
Rhodonea curves were named by the Italian mathematician Guido Grandi between the year 1723 and 1728.
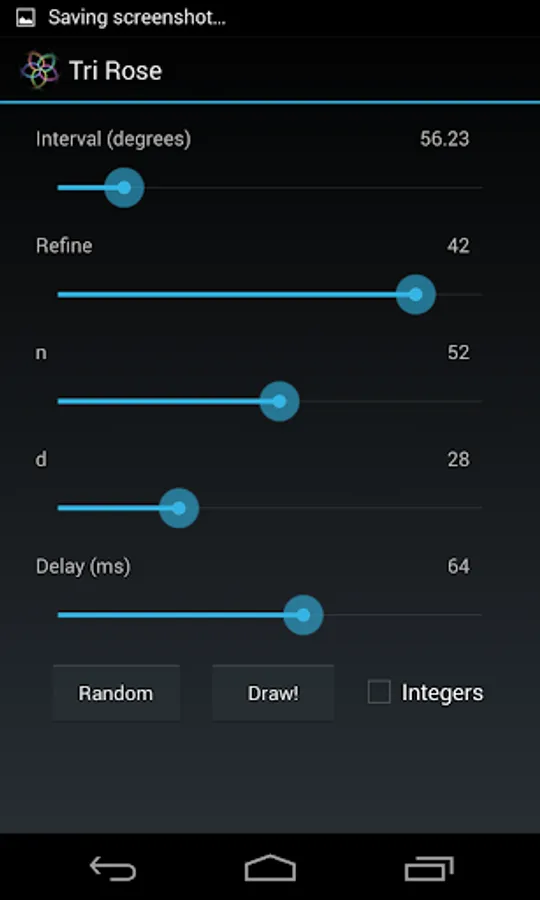
Tips on generating roses:
For integer n, the shape will appear similar to a flower. If n is odd half of these will overlap, forming a flower with n petals. However if it is even the petals will not overlap, forming a flower with 2n petals.
When d is a prime number then n/d is a least common form and the petals will stretch around to overlap other petals. The number of petals each one overlaps is equal to the how far through the sequence of primes this prime is +1, i.e. 2 is 2, 3 is 3, 5 is 4, 7 is 5, etc.
In the form k = 1/d when d is even then it will appear as a series of d/2 loops that meet at 2 small loops at the center touching (0, 0) from the vertical and is symmetrical about the x-axis. If d is odd then it will have d div 2 loops that meet at a small loop at the center from ether the left (when in the form d = 4n − 1) or the right (d = 4n + 1).
If d is not prime and n is not 1, then it will appear as a series of interlocking loops.
If k is an irrational number then the curve will have infinitely many petals, and it will be dense in the unit disc.
Mathematically generate unique and intricate rose graphs (rhodonea curves) and share them with your friends!
Rhodonea curves were named by the Italian mathematician Guido Grandi between the year 1723 and 1728.
Tips on generating roses:
For integer n, the shape will appear similar to a flower. If n is odd half of these will overlap, forming a flower with n petals. However if it is even the petals will not overlap, forming a flower with 2n petals.
When d is a prime number then n/d is a least common form and the petals will stretch around to overlap other petals. The number of petals each one overlaps is equal to the how far through the sequence of primes this prime is +1, i.e. 2 is 2, 3 is 3, 5 is 4, 7 is 5, etc.
In the form k = 1/d when d is even then it will appear as a series of d/2 loops that meet at 2 small loops at the center touching (0, 0) from the vertical and is symmetrical about the x-axis. If d is odd then it will have d div 2 loops that meet at a small loop at the center from ether the left (when in the form d = 4n − 1) or the right (d = 4n + 1).
If d is not prime and n is not 1, then it will appear as a series of interlocking loops.
If k is an irrational number then the curve will have infinitely many petals, and it will be dense in the unit disc.