About Capacitor Calculator
Capacitor Charge and Time Constant Calculator
Time constant is a measurement of the time needed to charge capacitor by ~63.2% or discharge a capacitor by ~36.8% of the differenece between the old value and new value after an impulse that induces a change has been applied. The time constant also defines the response of the circuit to a step (or constant) voltage input. Consequently, the cutoff frequency of the circuit is defined by the time constant.
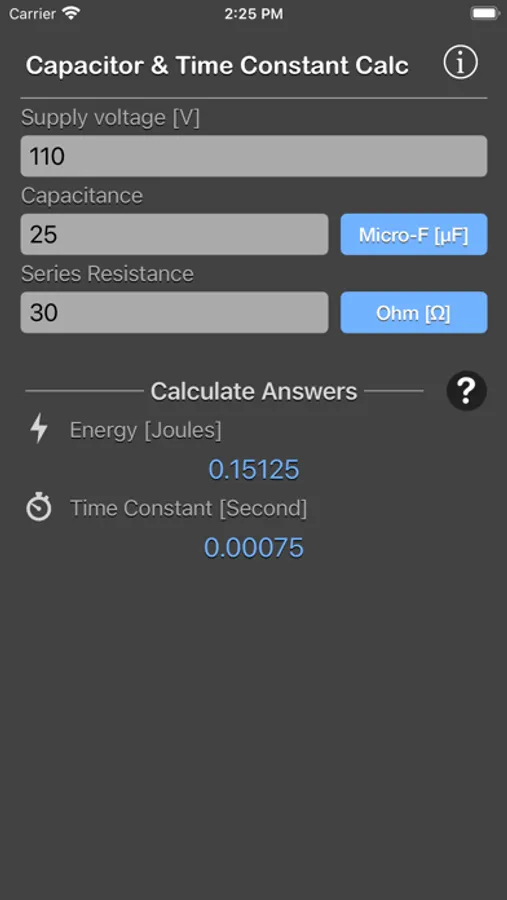
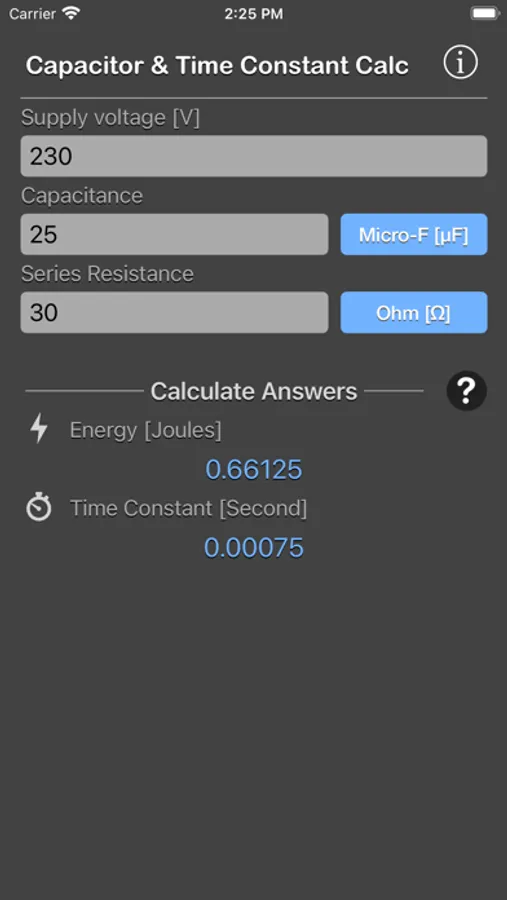
Time Constant = Voltage (V) x Capacitance (μF) x Load Resistance (Ω)
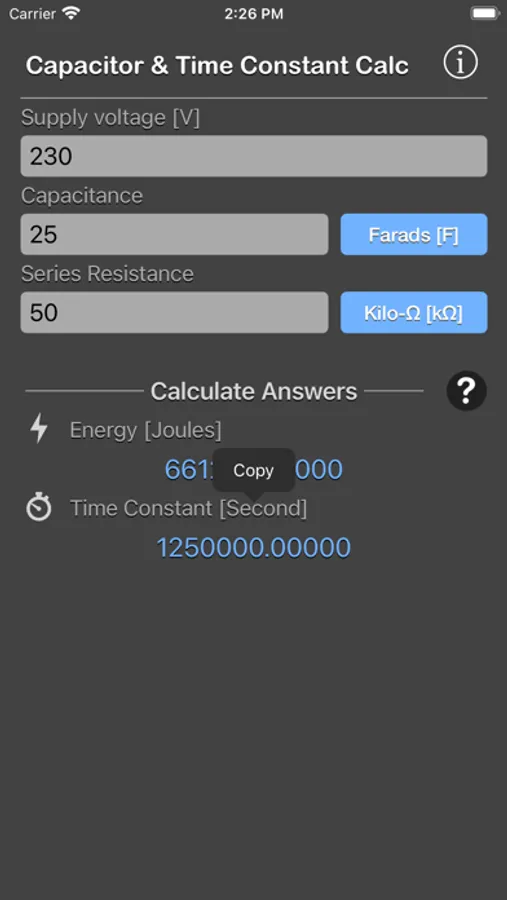
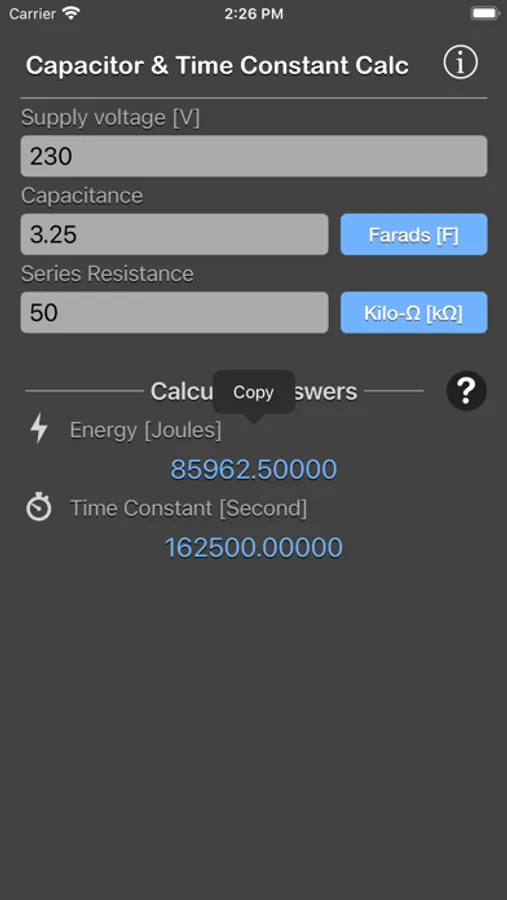
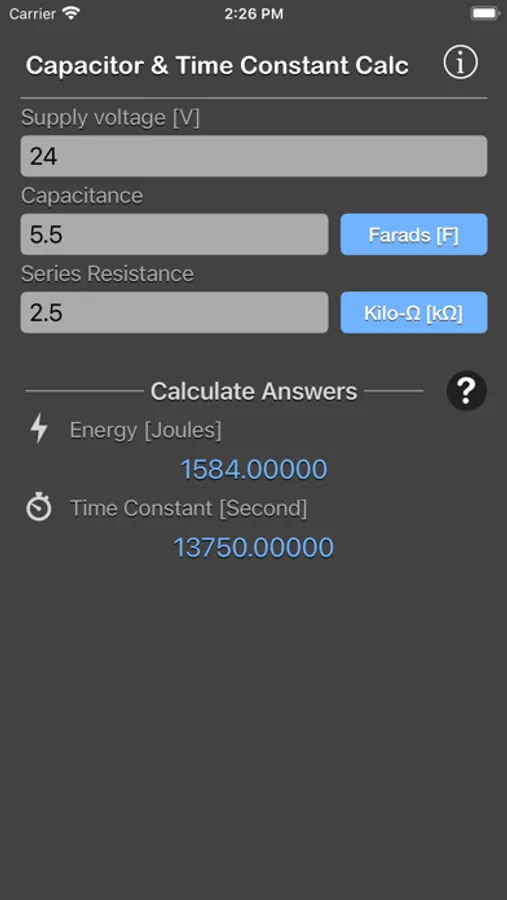
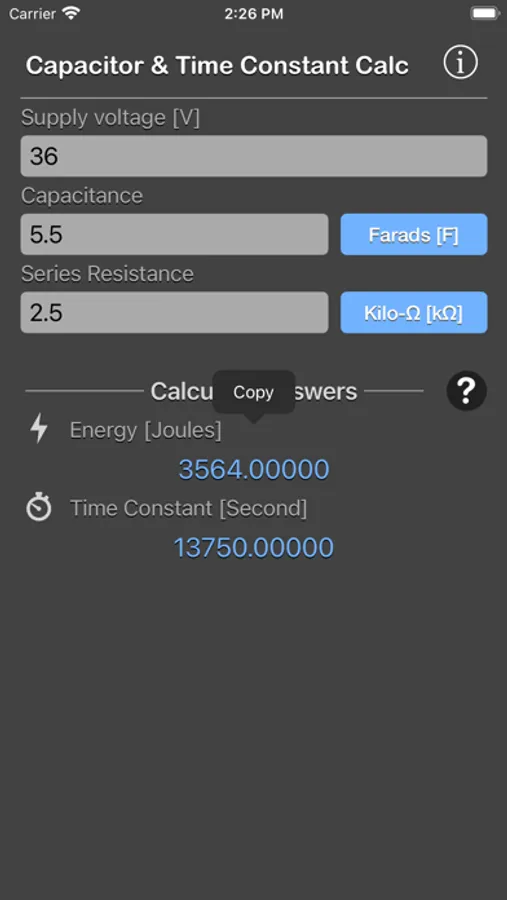
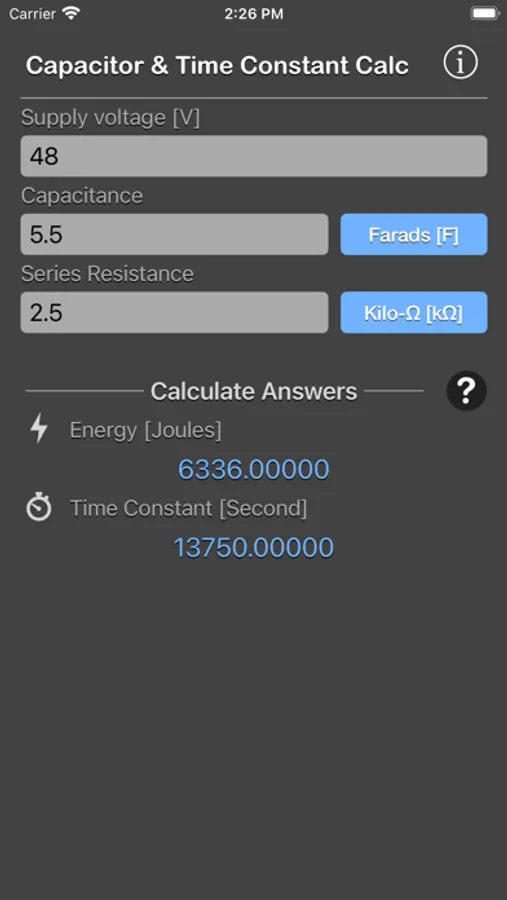
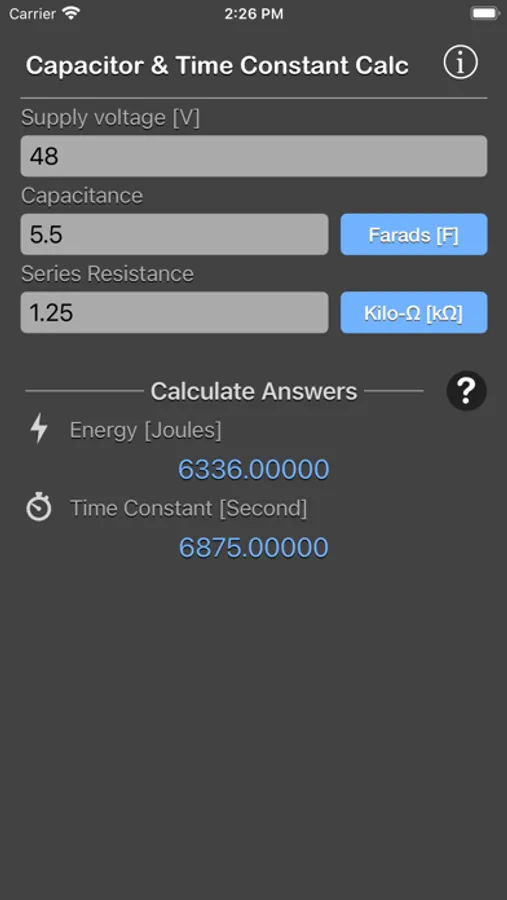
To calculate the energy (E) and time constant (RC) in a capacitor for the given voltage across it.
We need two different values from the calculator.
- Energy stored on a capacitor (E) can be determined by giving all three inputs: voltage (V), capacitance (C) and load resistance (R).
- Time constant (T) can be determined from the values of capacitance (C) and load resistance (R).
All Electrical or Electronic circuits or systems suffer from some form of “time-delay” between its input and output, when a signal or voltage, either continuous, ( DC ) or alternating ( AC ) is firstly applied to it.
This delay is generally known as the time delay or Time Constant of the circuit and it is the time response of the circuit when a step voltage or signal is firstly applied. The resultant time constant of any electronic circuit or system will mainly depend upon the reactive components either capacitive or inductive connected to it and is a measurement of the response time with units of, Tau – τ
When an increasing DC voltage is applied to a discharged Capacitor, the capacitor draws a charging current and "charges up", and when the voltage is reduced, the capacitor discharges in the opposite direction. Because capacitors are able to store electrical energy they act like small batteries and can store or release the energy as required.
The charge on the plates of the capacitor is given as: Q = CV. This charging (storage) and discharging (release) of a capacitors energy is never instant but takes a certain amount of time to occur with the time taken for the capacitor to charge or discharge to within a certain percentage of its maximum supply value being known as its Time Constant ( τ ).
Thanks for your support and do visit nitrio.com for more apps for your iOS devices.
Time constant is a measurement of the time needed to charge capacitor by ~63.2% or discharge a capacitor by ~36.8% of the differenece between the old value and new value after an impulse that induces a change has been applied. The time constant also defines the response of the circuit to a step (or constant) voltage input. Consequently, the cutoff frequency of the circuit is defined by the time constant.
Time Constant = Voltage (V) x Capacitance (μF) x Load Resistance (Ω)
To calculate the energy (E) and time constant (RC) in a capacitor for the given voltage across it.
We need two different values from the calculator.
- Energy stored on a capacitor (E) can be determined by giving all three inputs: voltage (V), capacitance (C) and load resistance (R).
- Time constant (T) can be determined from the values of capacitance (C) and load resistance (R).
All Electrical or Electronic circuits or systems suffer from some form of “time-delay” between its input and output, when a signal or voltage, either continuous, ( DC ) or alternating ( AC ) is firstly applied to it.
This delay is generally known as the time delay or Time Constant of the circuit and it is the time response of the circuit when a step voltage or signal is firstly applied. The resultant time constant of any electronic circuit or system will mainly depend upon the reactive components either capacitive or inductive connected to it and is a measurement of the response time with units of, Tau – τ
When an increasing DC voltage is applied to a discharged Capacitor, the capacitor draws a charging current and "charges up", and when the voltage is reduced, the capacitor discharges in the opposite direction. Because capacitors are able to store electrical energy they act like small batteries and can store or release the energy as required.
The charge on the plates of the capacitor is given as: Q = CV. This charging (storage) and discharging (release) of a capacitors energy is never instant but takes a certain amount of time to occur with the time taken for the capacitor to charge or discharge to within a certain percentage of its maximum supply value being known as its Time Constant ( τ ).
Thanks for your support and do visit nitrio.com for more apps for your iOS devices.