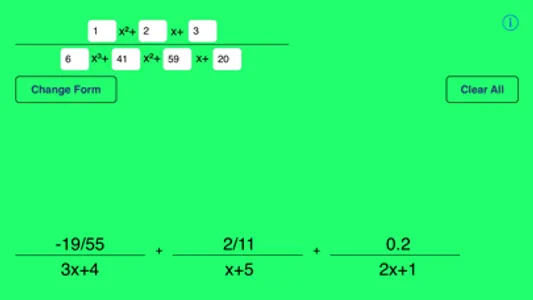
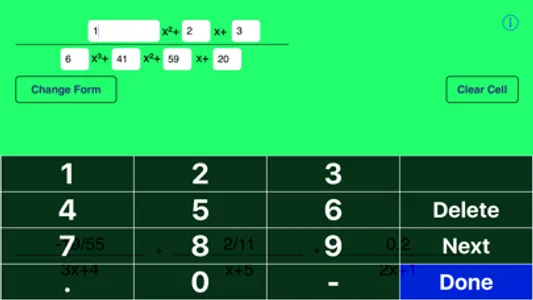
Partial Fractions is a handy way to compute partial fraction expansions. It works for 2nd and 3rd order denominators and supports many different input forms (listed below). Supports real and complex answers. It is very useful when trying to integrate fractions.
Fast and easy to use with a very smooth user interface. Does not require an internet connection.
Input Forms (Numerator):
• a
• ax+b
• ax^2+bx+c
• (ax+b)(cx+d)
Input Forms (Denominator):
• ax^2+bx+c
• (ax+b)(cx+d)
• (ax+b)^2
• ax^3+bx^2+cx+d
• (ax^3+bx+c)(dx+e)
• (ax+b)(cx+d)(ex+f)
• (ax+b)^2(cx+d)
• (ax+b)^3
Fast and easy to use with a very smooth user interface. Does not require an internet connection.
Input Forms (Numerator):
• a
• ax+b
• ax^2+bx+c
• (ax+b)(cx+d)
Input Forms (Denominator):
• ax^2+bx+c
• (ax+b)(cx+d)
• (ax+b)^2
• ax^3+bx^2+cx+d
• (ax^3+bx+c)(dx+e)
• (ax+b)(cx+d)(ex+f)
• (ax+b)^2(cx+d)
• (ax+b)^3
Show More