Kurvendiskussion
SysHil
$0.99
1+
downloads
About Kurvendiskussion
The app is deliberately kept simple to underline the meaning and purpose. Namely the representation of functions as graphics. The following functions are available in the parser and can be combined with brackets and dot-before-dash calculation.
f(x) = ... with the following identifiers:
- +, -, *, /, ^ (, ), PI
- x, x^2, ...,x^n
- a^x, a^(b*x), a^(b*x/c)
- sin(x), cos(x), tan(x)
- asin(x), acos(x), atan(x)
- sinh(x), cosh(x), tanh(x)
- asinh(x), acosh(x), atanh(x)
- sqrt(x), exp(x)
- ln(x), log(x)
- d(x), u(x), r(x)
f(x) = ... with the following identifiers:
- +, -, *, /, ^ (, ), PI
- x, x^2, ...,x^n
- a^x, a^(b*x), a^(b*x/c)
- sin(x), cos(x), tan(x)
- asin(x), acos(x), atan(x)
- sinh(x), cosh(x), tanh(x)
- asinh(x), acosh(x), atanh(x)
- sqrt(x), exp(x)
- ln(x), log(x)
- d(x), u(x), r(x)
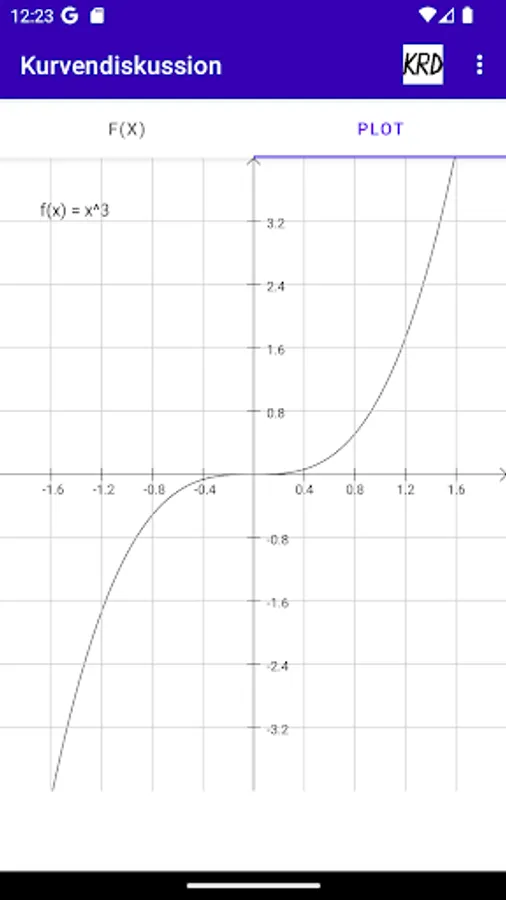
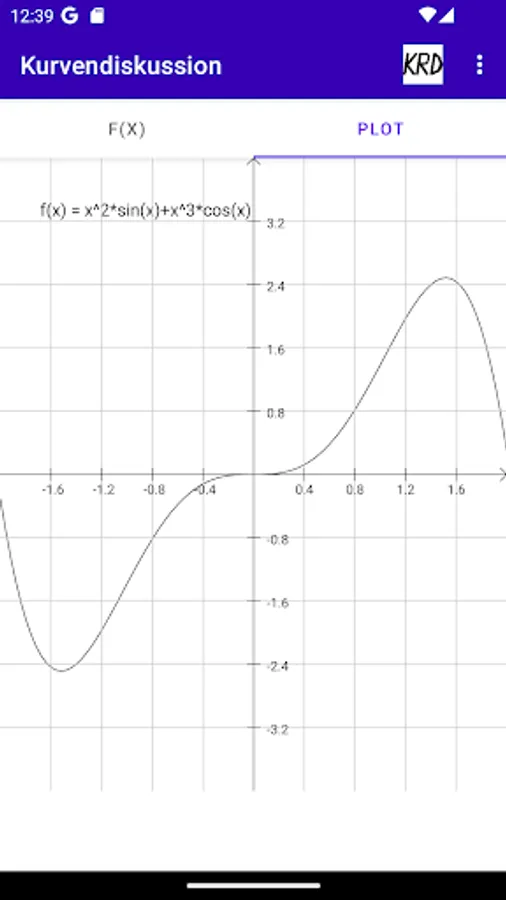
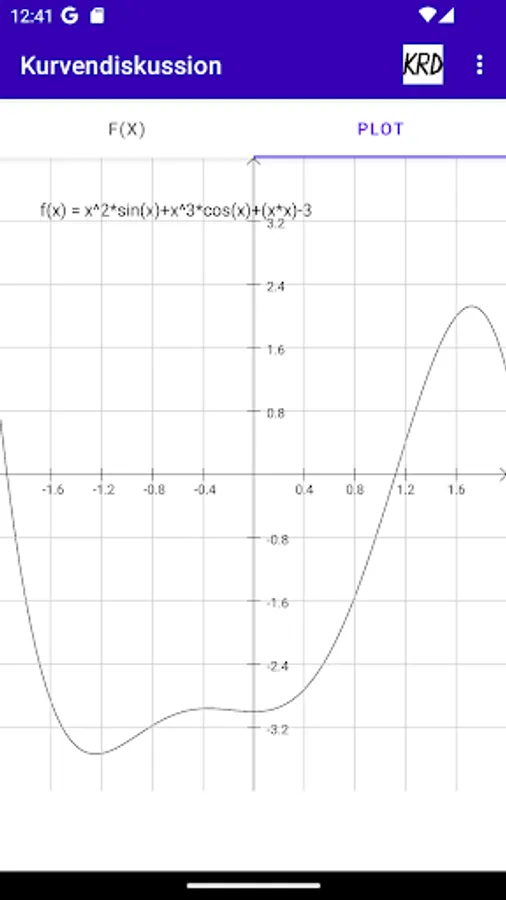
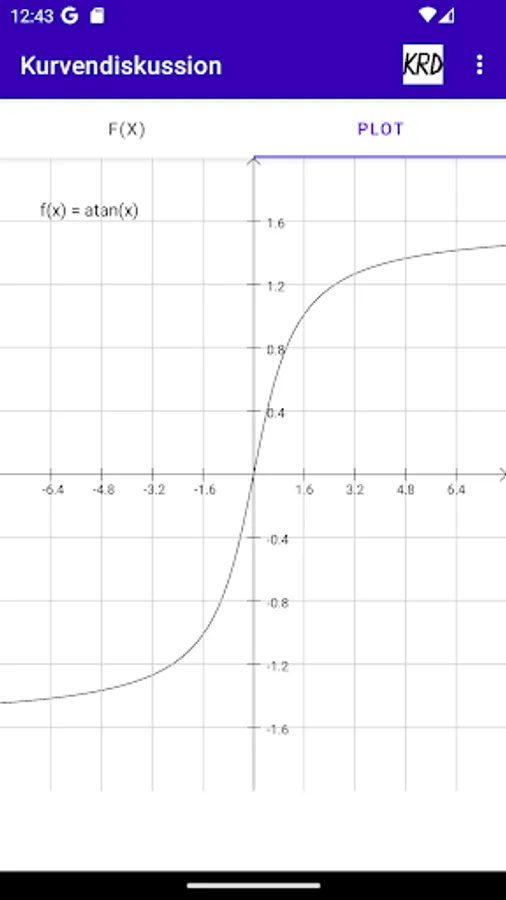
Kurvendiskussion Screenshots
Tap to Rate: