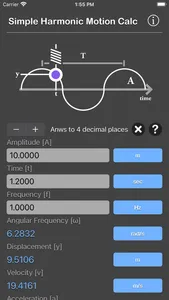
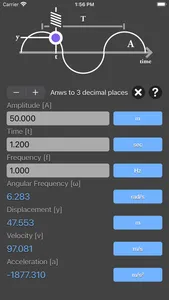
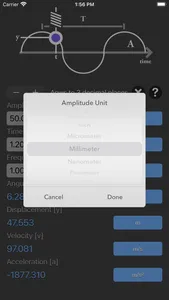
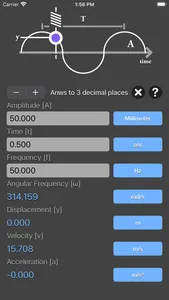
Simple Harmonic Motion Calculator are physic/math calculator to find amplitude of oscillations, angular frequency, frequency, time point to measure the displacement, displacement, velocity or acceleration fast and easy.
Features:
- Instant calculation
- Result are copy able to other app
- Formula are include as reference
- Support up to 16 decimal place
- Support various unit for each input
In mechanics and physics, simple harmonic motion is a special type of periodic motion or oscillation motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement.
Simple harmonic motion can serve as a mathematical model for a variety of motions, such as the oscillation of a spring. In addition, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum as well as molecular vibration. Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law. The motion is sinusoidal in time and demonstrates a single resonant frequency. For simple harmonic motion to be an accurate model for a pendulum, the net force on the object at the end of the pendulum must be proportional to the displacement. This is a good approximation when the angle of the swing is small.
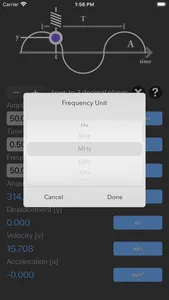
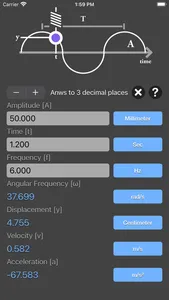
simple harmonic motion equations:
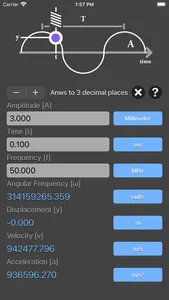
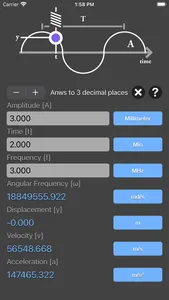
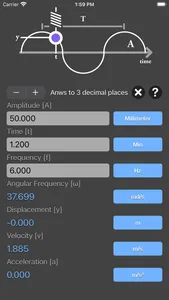
y = A * sin(ωt)
v = A * ω * cos(ωt)
a = - A * ω² * sin(ωt)
ω = 2πf
where:
A is the amplitude of oscillations
ω is the angular frequency of oscillations in rad/s
f is the frequency
t is the time point when you measure the particle's displacement
y is the displacement
v is the velocity,
a is the acceleration
Thanks for your support and do visit nitrio.com for more apps for your iOS devices.
Features:
- Instant calculation
- Result are copy able to other app
- Formula are include as reference
- Support up to 16 decimal place
- Support various unit for each input
In mechanics and physics, simple harmonic motion is a special type of periodic motion or oscillation motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement.
Simple harmonic motion can serve as a mathematical model for a variety of motions, such as the oscillation of a spring. In addition, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum as well as molecular vibration. Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law. The motion is sinusoidal in time and demonstrates a single resonant frequency. For simple harmonic motion to be an accurate model for a pendulum, the net force on the object at the end of the pendulum must be proportional to the displacement. This is a good approximation when the angle of the swing is small.
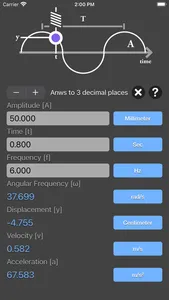
simple harmonic motion equations:
y = A * sin(ωt)
v = A * ω * cos(ωt)
a = - A * ω² * sin(ωt)
ω = 2πf
where:
A is the amplitude of oscillations
ω is the angular frequency of oscillations in rad/s
f is the frequency
t is the time point when you measure the particle's displacement
y is the displacement
v is the velocity,
a is the acceleration
Thanks for your support and do visit nitrio.com for more apps for your iOS devices.
Show More